欲 扬 先 抑

ABC 203

掉分了。

居然被 C 给卡了一下，又被 D 卡。

D

给定一个 $n \times n$ 的矩阵，求其中所有 $k \times k$ 的子矩阵的中位数的最小值。

首先想到的是大力数据结构，树套树之类的，可是这东西不一定过得了，而且 ABC 的 D 怎么可能要数据结构。

然后就想来想去奇奇怪怪的做法，一段时间想着这似乎可以二分，但是很快就被我判定没有二分性了，可能是受到了前面一题枚举被我误认成二分的影响吧。

所以我还不理解二分，对吗。/dk

其实是有二分性的。我们可以转化一下这样一个问题，把它要求的变成要求最小的数 $x$, 使存在至少一个 $k \times k$ 的矩阵中最多有 $\lfloor \frac{k^2}{2} \rfloor$ 个比其小，这样就显然可以二分的。

那么问题出在哪里呢？其实二分出来的不一定要是答案，只要最后的这个东西能成为答案就行了，所以我确实不理解二分（

#include <cstdio>
const int N = 805;
int n, k, a[N][N], sum[N][N], flag[N][N], ans;
bool check(int x) {
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)   
            flag[i][j] = a[i][j] <= x;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
            sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + flag[i][j];
    for(int i = 1; i <= n-k+1; i++)
        for(int j = 1; j <= n-k+1; j++) {
            int d = sum[i+k-1][j+k-1] - sum[i-1][j+k-1] - sum[i+k-1][j-1] + sum[i-1][j-1];
            if(d >= k*k-k*k/2) return true;
        }
    return false;
}
int main() {
    scanf("%d%d", &n, &k);
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++) scanf("%d", &a[i][j]);
    int l = 0, r = 1000000000;
    while(l <= r) {
        int mid = l + (r-l) / 2;
        if(check(mid)) ans = mid, r = mid - 1;
        else l = mid + 1;
    }
    printf("%d", ans);
    return 0;
}

Deltix Round, Spring 2021

这个比赛体验就顺利多了嘛！

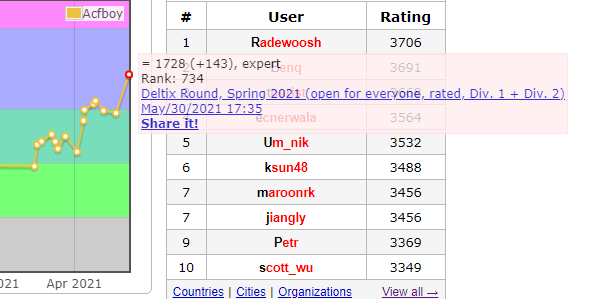
加143，加航143 ？这谐音妙哇！

成功 PB, 而且成了历史上上分最快的一次。

顺利的提交。

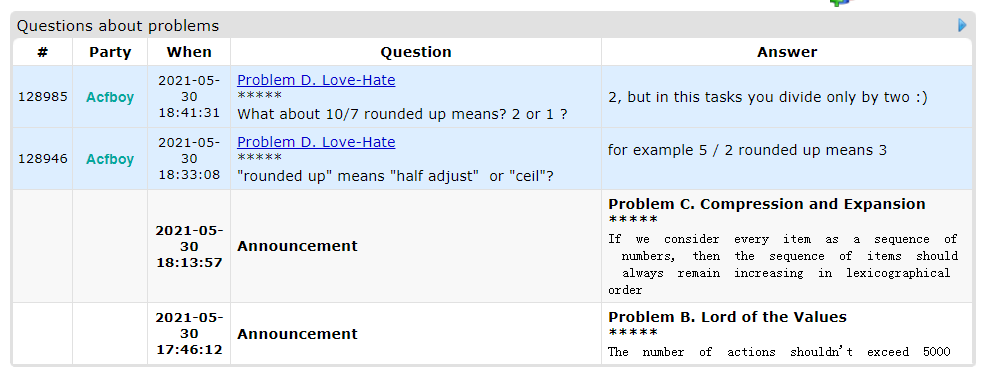
甚至还达成了第一次提问，不过这个问题有点傻，晚上脑子比较糊涂。

"rounded up 是上取整还是四舍五入？"

"举个例子， 5/2 rounded up 的结果是 $3$"

"那 10/7 是 $2$ 还是 $1$ 呢？"

"$2$, 但是题目里只要去你除以二 😃"

A

直接模拟即可，因为有意义的变化显然不会超过 $n$ 次。

B

保证输入的数据个数是偶数，所以若两个之间一定可以，那么 $n$ 个也一定可以。

设第一个为 $a$, 第二个为 $b$, 然后搞一搞就可以发现一定可以。

核心代码。

	for(int i = 1; i <= n; i += 2) {
            printf("%d %d %d\n", 1, i, i+1);
            printf("%d %d %d\n", 2, i, i+1);
            printf("%d %d %d\n", 2, i, i+1);
            printf("%d %d %d\n", 1, i, i+1);
            printf("%d %d %d\n", 2, i, i+1);
            printf("%d %d %d\n", 2, i, i+1);
        }

C

搞个栈，若是 $1$ 直接新建一层，若能接上直接把当前层加一，接不上就后退一层即可。

那么若有两种情况都满足要求怎么办？其实根本就不需要考虑这样的情况，因为你外面可以接下去，里面也一定可以接下去，直到接不下去的时候退回来不管怎么样都是要退的。

代码。

#include <cstdio>
const int N = 1005;
int T, n, x, st[N], top;
int main() {
    scanf("%d", &T);
    while(T--) {
        top = 0;
        scanf("%d", &n);
        for(int i = 1; i <= n; i++) {
            scanf("%d", &x);
            if(x == 1) st[++top] = 1;
            else {
                while(x != st[top] + 1) top--;
                st[top] ++;
            }
            for(int j = 1; j < top; j++) printf("%d.", st[j]);
            printf("%d\n", st[top]);
        }
    }
    return 0;
}

D

D ……就不会了。

其实能上那么多分完全是运气好，因为 D 难度一下子增加的太大，导致区分度降低，我前面写得比较快，于是排名就高了，而且这又是一个 Div1 + Div2, 所以分数就升得更多。

赛后解决 D.居然是随机化，不过是确保正确的随机化。

twt-tec 有 $m$ 个产品。$n$ 个人，每个人喜欢 twt-tec 的一些产品，最多不会喜欢超过 $p$ 个，求最大的 twt-tec 产品子集，使得有至少一半（上取整）的人喜欢这些产品。

$n \le 10^5, p \le 15, m \le 60$

看着这个数据范围就想着状压之类的东西，但是没有什么用。这子集肯定不能作状态，而不作状态又会有后效性。

然后注意到 $p \le 15$ 这个条件，于是猜测最后的答案和输入的有一定的关系。但是赛场上我想到了答案可能是某一个人喜欢的，但这很快就被否决了，因为样例都过不了。

其实这就是关键点。

答案肯定是一个人喜欢的东西的子集。而题目又要求至少要有一半的人喜欢这些产品，所以我们随便选一个，就有 $\frac{1}{2}$ 的概率选到包含答案的集合，把这个过程重复 $t$ 次，没有选到包含答案的集合的概率就只有 $\left(\frac{1}{2}\right)^t$, 这非常的小。按照官方题解的说法就是这个概率比你现在被陨石砸中的概率还要小

那么考虑缩小了范围后怎么找答案。可以枚举 $p$ 个的子集，然后判断一下 $n$ 个里面有多少人喜欢这个，然后来更新答案就可以了。

但是 $n3^n$ 是过不了的，所以不能直接去枚举。可以设置 $cnt_s$ 表示喜欢的产品集合与 $p$ 个组成的集合的交集为 $s$ 的人有多少个。然后从小到大合并一下就可以了。

代码。一个很坑的地方是 rand() 的范围只到 $32768$, 所以要么使用极不均匀的 rand()*rand(), 要么使用高科技的 mt19937。后者要 c++11, NOIP 不能用，所以我还是用了 rand()*rand()。但这个似乎被 hack 伪随机数了。

#include <cstdio>
#include <ctime>
#include <cstdlib>
#include <vector>
const int N = 200005, M = 65, P = 16;
int n, m, p, sum[1 << P], max = -1;
char a[N][M], ans[M];
std::vector<int> t;
int popcount(int x) { return !x ? 0 : (popcount(x & (x-1)) + 1); }
int main() {
	srand(time(0));
	scanf("%d%d%d", &n, &m, &p);
	for(int i = 1; i <= n; i++)
		scanf("%s", a[i]);
	for(int T = 1; T <= 20; T++) {
		int u = rand()*rand() % n + 1;
		t.clear();
		for(int i = 0; i < m; i++)
			if(a[u][i] == '1') t.push_back(i);
		int p = t.size();
		for(int i = 1; i <= n; i++) {
			int v = 0;
			for(int j = 0; j < p; j++)
				if(a[i][t[j]] == '1') v |= 1 << j;
			sum[v] ++;
		}
		for(int i = 0; i < p; i++)
			for(int s = 0; s < (1 << p); s++)
				if(!(s & (1 << i))) sum[s] += sum[s | (1 << i)];
		for(int s = 0; s < (1 << p); s++)
			if(sum[s] >= (n+1)/2 && popcount(s) > max) {
				max = popcount(s);
				for(int j = 0; j < m; j++) ans[j] = '0';
				for(int j = 0; j < p; j++)
					if(s & (1 << j)) ans[t[j]] = '1';
			}
		for(int i = 0; i < (1 << p); i++) sum[i] = 0;
	}
	printf("%s", ans);
	return 0;
}

E

读 错 题 了 ！

开始时 $n$ 盏灯都是灭的，谭炜谭点灯大师会每次等概率随机选择一盏灭掉的灯点亮，求到第一次存在连续的一段 $k$ 盏灯中被点亮了多盏时的期望亮灯数。

概率题，本质上是组合计数。

首先，若亮了 $p$ 盏灯，一共有 ${n \choose p}$ 种情况，那么每种情况出现的概率是 $\frac{1}{n\choose p}$。剩下就是要求任意连续 $k$ 个不存在多个球被选中的情况。情况数是

$n - (p-1)\times (k-1) \choose p$

因为两个选出的相隔至少是 $k-1$ 个，然后要有 $p-1$ 个间隔，所以要在剩下的中选出 $p$ 个来。

把两个东西乘起来就是选了 $p$ 盏灯出现满足条件的情况的概率，对其求和可以得到期望。

代数推导感谢 @wxy_，在 这里。

其实就是把每步分开来处理，因为每次对答案的贡献都是 $1$, 然后我们求的方案数就是有多少种方案活到而来这一步，而这每一个对答案的贡献都是 $1$, 再除以每一个的概率，就是它们对期望的贡献。

Hack !

好耶！被 zjk 叉掉了！

他叉掉了我的 D 题，代码如下：

#include <bits/stdc++.h>
const int N = 2e5 + 2;
int a[N], b[N], n;
int main() {
    n = 2e5;
    int yy = 1622449900;
    for (int i = yy; i <= yy + 1000; i++) {
        srand(i);
        for (int i = 1; i <= 100; ++i) a[(rand() * rand()) % n] = 1;
    }
    printf("%d 2 2\n", n);
    for (int i = 0; i < n; i++)
        if (a[i]) puts("00");
        else puts("11");
}

原理是这样的：因为数据规模是 $10^5$, 而 time(0) 在一秒内只会有 $1000$ 个不同的种子出来，把这些种子所生成的随机数的位上全部变成 00, 其它全部变成 11, 就可以叉掉这 $100$ 秒以内的提交，因为我们只会随机到这些 00 上。

同样，用 mt19937 也会遇上这个问题，所以得使用更高精度的时间作为种子，这样在一秒内有较大的不同种子才不会被叉掉。

#include <random>
#include <chrono>
std::mt19937 rnd(std::chrono::steady_clock::now().time_since_epoch().count());

记得开 c++11。

不过 ccf 的比赛里尽管用 time(0) 和 rand() 就好了，他不会设计数据来卡你，要是卡了，嘿嘿，那就好玩了。